8．集団における遺伝子

---

このページの内容

遺伝子頻度と遺伝子型頻度 遺伝子頻度と遺伝子型頻度の求め方 ハーディ・ワインベルグの法則 遺伝子頻度に影響を与える要因 選抜 移入 近親交配 突然変異 機会的遺伝浮動 集団の有効な大きさ

メンデルの遺伝法則を理解すると，遺伝子型が分っている両親の交配によって得られる子供の遺伝子型と表現型の分布が予測できる。

たとえば，無角遺伝子をヘテロでもつウシ（Pp×Pp）の交配によって，子世代には1PP：2Pp：1ppの遺伝子型比が生じるものと予測できる。

さらにPはpに対して優性なので，表現型の分布は3無角：1有角と予測される。

家畜育種においては，集団内での交配によって生まれる子孫の表現型と遺伝子型の頻度を予測するために，いろいろな遺伝子型をもつ個体間における交配の確率を知る必要がある。

例を挙げてみよう。遺伝子型PP，Ppならびにppをもつ個体の集団において，たとえば，PPオスとppメスとの交配によって生まれくる子ウシの割合を予測するためには，当該の遺伝子型をもつ親ウシ間での交配の頻度を知らなければならない。

集団遺伝学は集団内の遺伝子頻度と遺伝子型頻度を調べ，その後の世代でそれらの頻度がどのように変化するのかを予測する研究領域である。
 

 

8-1．遺伝子頻度と遺伝子型頻度

8-1-1．遺伝子型頻度

遺伝子型頻度は，集団内において特定の遺伝子型をもつ個体の割合と定義される。いま，無角ウシと有角ウシの集団において，それぞれの遺伝子型をもつ個体の数をnで，それぞれの遺伝子型を下付き文字で表わすと，

n_PP＝無角遺伝子をホモでもつ個体数（PP）
n_Pp＝無角遺伝子をヘテロでもつ個体数（Pp）
n_pp＝有角遺伝子をホモでもつ個体数（pp）

遺伝子型頻度は，

f(PP)＝n_PP/n
f(Pp)＝n_Pp/n
f(pp)＝n_pp/n

そして，すべての頻度の合計は1に等しい。

f(PP)＋f(Pp)＋f(pp)＝1

 

ここで， f(P)とは遺伝子Pの頻度を， f(PP)とは遺伝子型PPの頻度を表す。 fはfrequencyの略。

8-1-2．遺伝子頻度

遺伝子頻度はある集団における各々の対立遺伝子の相対的頻度と定義される。いま，n_Pを集団内の遺伝子Pの数とすると，

f(P)＝n_P/2n

遺伝子Pの数は無角ホモの個体数を2倍（各個体は2個のP遺伝子をもつ）したものと，無角ヘテロの個体数（各個体は1個のP遺伝子をもつ）の和として求められる。

n_P＝2n_PP　＋　n_Pp

同様に，n_pはヘテロ個体数と有角個体数の2倍したものの和となる。

n_p＝n_Pp　＋　2n_pp

遺伝子頻度は遺伝子型頻度からも求めることができる。

f(P)＝f(PP)　+　(1/2)(Pp)
f(p)＝(1/2)(Pp)　+　f(pp)

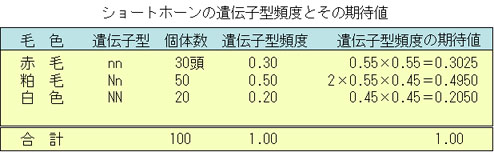
例8-1では，ショートホーンにおける毛色の遺伝子頻度と遺伝子型頻度の計算例を示す。

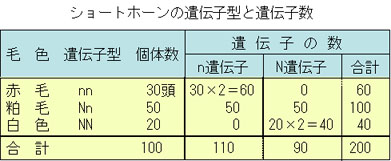
ここにショートホーン 100頭の集団があり，その毛色は赤色30頭，粕毛50頭，白色20頭であった。ショートホーンの毛色の遺伝子型は，赤色nn，粕毛Nn，白色NNである。この集団におけるnとNの遺伝子頻度，それぞれpとqを求めてみよう。

遺伝子頻度の求め方
赤色遺伝子nの頻度は表にみられるように，

遺伝子数が30×2＋50＝110で，この遺伝子座全体の遺伝子数が100×2＝200であるから，

p＝110/200
＝0.55

同様に，

q＝90/200
＝0.45

そして，
p＋q＝1
となる。

遺伝子型頻度の求め方
例8-1では，

• 赤色牛の遺伝子頻度　0.30
• 粕毛牛の遺伝子頻度　0.50
• 白色牛の遺伝子頻度　0.20

であった。

nとNの遺伝子頻度はそれぞれpとqであるが，各遺伝子型頻度は無作為交配の場合，
（pn＋qN）²＝p²nn＋2pqNn＋q²NN
の各項に対応する。

上記のようにして求めた遺伝子型頻度の期待値は，頭数の比率から求めた遺伝子型頻度ときわめてよく一致する。

 

 

8-2．ハーディ・ワインベルグの法則

メンデルの研究が1900年に再発見されると，科学者は進化論を粒子遺伝理論で説明し始めようとした。
1つの疑問は，ある世代から次の世代に移る際に遺伝子頻度と遺伝子型頻度に何が起こるのかということであった。

1908年にG.H. HardyとW. Weingergがそれぞれ独自に，ある仮定の下での世代を越えた遺伝子頻度と遺伝子型頻度との間の基本的な関係を明らかにした。

これをハーディ・ワインべルグの法則といい，次のようにまとめられる。

『交配が無作為に行われている大きな集団では，遺伝子頻度を変化させる作用（突然変異，移入ならびに選抜など）が働かなければ，遺伝子頻度と遺伝子型頻度は何世代経っても一定であり，遺伝子型頻度は遺伝子頻度の二項式展開〔先の例は(0.55＋0.45)2＝0.3025＋0.4950＋0.2025〕で与えられる。』

遺伝子頻度と遺伝子型頻度が集団内で一定である時，これを「平衡に達している」という。

平衡に必要な条件は，以下の通りである。

1. 大きな集団である。
2. 無作為交配が行われている。
3. 遺伝子頻度を変化させるような作用がない。

 

8-2-1．ハーディ・ワインべルグの平衡時の遺伝子頻度と遺伝子型頻度

2つの遺伝子をもつ単一の遺伝子座がハーディ・ワインべルグの平衡に達している集団では，遺伝子頻度と遺伝子型頻度に明らかな関係が認められる。今ここで，f(B)＝pとf(b)＝qで平衡に達している集団を考えてみよう。

遺伝子型頻度は，

このことは，

• 遺伝子型BBの頻度は遺伝子Bの頻度の二乗に等しい。
• ヘテロ接合体Bbの頻度は遺伝子Bとbの頻度の積の2倍に等しい。
• 遺伝子型bbの頻度は遺伝子bの頻度の二乗に等しい。

遺伝子頻度と遺伝子型頻度との間になぜ特別の関係が成り立つのであろうか？

ハーディ・ワインべルグの法則下では，遺伝子は無作為に2つずつ組み合わされる。
父親または母親の全体の遺伝子プールから遺伝子Bを引き出す確率がpであり，遺伝子bを引き出す確率がqである。
各遺伝子型は2つの遺伝子からなるので，遺伝子Bを2つもつ確率はp×p，すなわちpの二乗となる。

これらの遺伝子型頻度は，二項分布の展開によっても求めることができる。
(pB＋qb)²＝p²BB＋2pqBb＋q²bb

Bまたはｂを引き出す確率の合計は1である。

p＋q＝1

同様にすべての事象の頻度の合計も1に等しいはずである。
p²BB＋2pqBb＋q²bb＝1

遺伝子頻度と遺伝子型頻度が世代を越えて一定であるということは簡単に示すことができる。

オスとメスの配偶子のプール[集まり]において，遺伝子Bの頻度はpで，遺伝子bのそれはqである。
これらの配偶子が無作為に結合すると，受精して生じた接合子は次の4つの組み合わせとなる。

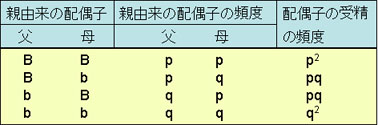
したがって，子孫では，
f(BB)＝p²
f(Bb)＝pq＋pq＝2pq
f(bb)＝q²
であり，親集団における頻度と同一となる。

遺伝子頻度も同一で，
f(B)＝f(BB)＋(1/2)f(Bb)
＝p²＋pq

これを代数的に整理すると，
＝p(p＋q）
＝p　　　(∴p＋q＝1）

同様に，
f(b)＝(1/2)f(Bb)＋f(bb)
＝pq＋q²
＝q(p＋q）
＝q　　　(∴p＋q＝1）

 

8-2-2．ハーディ・ワインべルグの法則の例

例8-2　親AAとaaの交配に始まる3世代について遺伝子頻度をみてみよう。
Aの遺伝子頻度とaの遺伝子頻度をそれぞれpとqとし，いずれも0.5ずつとする。p＋q＝1である。

次表に結果を示すが，2代，3代経ても遺伝子頻度は変化せず，p：q＝0.5：0.5＝1:1である。

 

 

8-3．遺伝子頻度に影響を与える要因

8-3-1．選抜

前述のようなハーディ・ワインベルグの法則が適用されているショートホーンの集団の毛色の遺伝子頻度と遺伝子型頻度が，選抜によってどの様に変化するかを検討してみよう。

赤毛遺伝子pnおよび白毛遺伝子qNの頻度をそれぞれ，前記の例にしたがって，0.55と0.45とする。
ここで，白色牛は全部繁殖させず，赤毛と粕毛のみが次代を生産したとする。

つまり，白色牛を除くという選抜を実施したとすると，次表に示すように白色牛はいなくなるから，赤毛と粕毛のみの遺伝子型頻度は，それぞれ0.3793と0.6207となる。

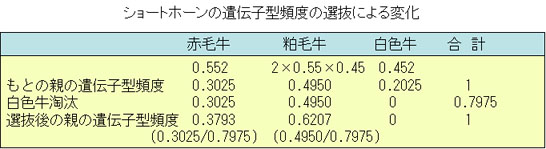
0.3793 はp²nnであり，0.6207は2pqnN に相当するから，ここから新しいp_n’とq_N’を計算すると，
p_n’＝(37.93×2＋62.07)÷200＝0.68965
q_N’＝62.07÷200＝0.31035
と求められる。

もっとも，
p_n’＝（0.3025×2＋0.4950)/(0.7975×2)
＝0.689655

q_N’＝0.4950/(0.7975×2)
＝0.31034

で求められれば，数値のまるめがないのでより正確な値が得られる。

すなわち，赤毛遺伝子頻度は0.6897となって，選抜前の0.55より0.1397多い頻度となり，白色遺伝子は逆に0.45－0.3103と0.1397少なくなるのである。

次代の遺伝子頻度は，（0.6897n＋0.3104N)²となるので，次表に示すように，赤毛牛が増加し，粕毛と白色牛が減少する。

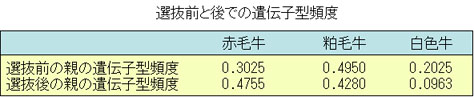
このように，特別の遺伝子型の種畜を除いたり，選んだりすることによって，次の世代の遺伝子頻度が望む方向に変化することが明かである。また，同時に遺伝子型頻度も変わってくるのである。
 

 

8-3-2．移入

積極的に遺伝子を外部から導入し，手持ちの家畜集団を改良していく場合などがある。たとえば，A品種の集団にB品種のオスが累進交配 grading-up 用に導入されたような場合は，もとのA品種の遺伝子頻度は当然次代で変化する。

 

 

8-3-3．近親交配

近親交配 inbreeding すると遺伝子頻度が変化する。すなわち，ホモ接合体が増加する。
近親交配を行うと，受胎率，生存率，産卵率，泌乳能力などの経済形質が低下する。これを近交退化 inbreeding depression という。

8-3-4．突然変異

希に起こる単発的な突然変異の場合はその遺伝子が次代に残る確率は0.63で，さらに次の世代に残る確率は減少していくから，特別にその突然変異遺伝子 mutational gene を取り出すということをしない限り問題にならない。

繰り返し生ずる突然変異の場合は，集団の遺伝子頻度に一定の影響があるが，家畜での自然突然変異率は10^-5～10^-6であるから，家畜育種の面からは余り問題にしなくてよい。

また，γ線の照射などで有用な突然変異を作り出し，その遺伝子の選抜に成功した例は家畜では知られていない。
 

 

8-3-5．機会的遺伝浮動

2つの相同遺伝子のうち，次世代に伝えられる遺伝子がどちらになるかは，もし，子が１頭しか生まれないなら偶然性によって決まる。
したがって，何頭かの親を考えるなら，ある遺伝子の方が多く次の世代に伝えられるということが起こりうる。

この偏りは，集団が大きければ問題はないが，小さい集団では，遺伝子頻度を変化させる要因となりうる。このような配偶子の機会的な抽出にともなう遺伝子頻度の変動を，機会的遺伝浮動 random genetic drift と呼んでいる。

われわれが実験的に小集団での選抜実験を行うとき，結果の再現性が得られないのは，この効果が大きいためであり，家畜育種でも注意する必要がある。
 

 

8-4．集団の有効な大きさ

一般の家畜の集団では雄の数は雌の数よりも少ないのが普通である。

このような集団では，近縁同士の交配を注意深く避けたとしても，同じ大きさの雌雄同数の無作為交配集団に比べれば，その遺伝的多様性は少なくなる。

したがって，現実の家畜の繁殖集団を，理想的なメンデル集団と比較したとき，その集団がその程度の大きさの理想集団と同一の遺伝効果をもっているかの換算を行ったものが集団の有効な大きさと呼ばれ，通常Neで示される。

実際の家畜の集団でNeが問題にされるのは，集団の遺伝的均一性（近交係数で表される）の増加が毎世代次のようになるからである。

たとえば，毎世代5頭の種雄牛と100頭の雌牛が無作為に交配されたとすると，実際の集団の頭数は105頭であるが，集団の有効な大きさNe＝19.05から19頭となる。

したがって，この集団では毎世代近交係数の上昇となって，2.6%ずつ平均近交係数が上昇する。

繁殖技術の発展により，少数の種雄牛による繁殖が行われている。これは改良上有効な面をもつが，一方で集団の近交度を高め，近交退化を生ずる可能性も存在するから，集団の有効な大きさに関する情報にも注意しておかなければならない。

 

---

最初に戻る

---

メニューのページへ戻る

家畜繁殖学 家畜育種学 参考文献

February 03, 2020