9b．遺伝的価値と人為的選抜

このページの内容

遺伝子型値と集団の平均 選抜と選抜反応 育種価 優性偏差 分散

---

人為的選抜は，家畜の外貌や生産性を劇的に変化させるために人類が用いる手段である。一般に行われる選抜の多くは家畜の性能に対してである。すなわち，

• 乳牛における泌乳量の増加
• 肉用家畜の離乳時における体重増加
• 一腹子数のような繁殖形質

などの改良のために選抜が行われている。

これらの形質の遺伝子型は表現型の測定値に影響する。特定形質について，子畜の平均能力に対する人為的選抜の影響を正確に知る必要がある。

この章では遺伝的な価値（遺伝子型値），集団の平均と分散，測定形質について期待される子畜の能力に対する人為的選抜の影響について学習する。

9-1．遺伝子型値と集団の平均

遺伝子型値と集団平均は次の例のように定義される。たとえば，血清中のホルモンの量(ml)がある遺伝子座位の遺伝子型によって影響されるとする。集団では表に示したように遺伝子頻度と表現型値が平衡に達しているとする。

対立遺伝子は下付文字で区別して表わし，遺伝子B₁はB₂に比べホルモン量を増加させるものとする。
表現型Pの下付文字は遺伝子型を構成する対立遺伝子を示す。個体の遺伝子型は表現型値として測定されたホルモン量に影響する。
このように，ある形質に対して遺伝子型によって特定の値が決まる。

遺伝子型値 genetic value は2つのホモ型の表現型，すなわちP₁₁とP₂₂の平均からの偏差と定義される。

平均値をmとすると，
m＝(P₁₁＋P₂₂)/2
となる。

この例ではm＝9 unitsで，3つの遺伝子型の遺伝子型値は

mは2つのホモ型の遺伝子型が影響した表現型の平均値と定義されるので， B₂B₂の遺伝子型値（すなわち，－a）はB₁B₁の遺伝子型値（a）に対し負の値をとる。
このようにa，d，－aという遺伝子型値を用いることによって，集団の平均ならびに分散に対する一般式が得られる利点がある。
aに対するdの関係は，以下に示すようないろいろな優性の程度として考えることができる。

 

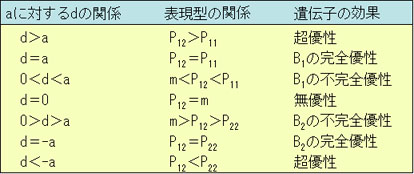
遺伝子型値といろいろな優性の程度の関係を次図にも示す。

各表現型は次の式で表わすことができる。
P_ij＝m＋V_ij
この式には，表現型に対する環境の影響（後で学習する）や表現型値を測定する際の誤差は考慮されていない。

集団平均：測定された集団のパラメータの一つが表現型値の平均値で，これをμで表す。平均値μはすべての表現型値の合計を観察個体数で除して求められる。

単一遺伝子座位の例では，
μ＝f(B₁B₁)P₁₁+f(B₁B₂)P₁₂＋f(B₂B₂)P₂₂

たとえば，ハーディ･ワインベルグの平衡に達している集団平均μは
μ＝P²P₁₁＋2pqP₁₂＋q²P₂₂

たとえば，P11をm+aというように各表現型値に標準化した遺伝子型値を代入すると，
μ＝p²(m＋a)＋2pq(m＋d)＋q²(m－a)
＝m(p²＋2pq＋q²)＋a(p²－q²)＋2pqd

p²＋2pq＋q²＝１，(p²－q²)＝(p＋q)(p－q)＝p－qなので，
集団の平均は，
μ＝m＋［a(p－q)＋2pqd］
となる。

この式で求められる集団平均は，確定した項mと平均遺伝子型値［a(p－q)＋2pqd］の和として表せる。
とくに，［a(p－q)＋2pqd］の項は遺伝子頻度に影響する選抜によって変化する。

ホルモンの例では，f(B₁)が増大すれば，集団の平均ホルモン量が増加する。
たとえば，m＝9，a＝3，d＝1とすれば，次のようになる。

9-2．選抜と選抜反応

選抜計画を策定する第一段階は選抜によって達成したい目標を決定することである。

ホルモンの例では，集団平均を上げることを目標とすると，1つの戦略として，繁殖集団からB₂B₂のホモ型の個体をすべて淘汰するということになる。

まず，第1世代の遺伝子頻度をp＝0.5とすると，選抜前の遺伝子頻度は，

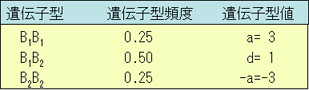
この世代の平均μは9.5である。ここで，すべてのB₂B₂のホモ型個体を淘汰すると，残された個体における遺伝子頻度は
p₁＝1/(1+q)
＝2/3
となる。

残りの個体を無作為交配したとすると，選抜後の子世代の遺伝子型頻度は次表のようになる。

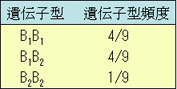
子世代の平均値μ₁は，
μ₁＝m＋a(p₁－q₁)＋2p₁q₁d
＝9＋3(2/3－1/3)＋2(2/3)(1/3)(1)
＝10.44

選抜反応をΔμと表記すると，親世代から子世代への集団の平均の変化は，
Δμ＝μ₁－μ＝0.94

mが一定なので，平均の変化はB₁遺伝子の頻度が増大したことによる平均遺伝子型値が上昇したためである。

この例で，もしB₁B₁個体だけを残そうとすると，子世代の集団平均は12.0になる。
遺伝子B₁が子世代に固定されるようになると，その後選抜に対して反応はもう起こらない。

この形質は‘遺伝的限界に達した’といえる。

9-3．育種価

単一遺伝子座を例にとると，個体の表現型にみられる違いは遺伝子型値の効果によるものである。

たとえば，
P₁₁－P₂₂＝(m+a)-(m-a)＝2a
について考えてみる。

完全優性ではP₁₁＝P₁₂なので，これらの個体は同じ表現型値を示す。
しかし，両親が子世代に彼らの遺伝子型を伝えるのではなく，むしろ子世代の各遺伝子座に1つの遺伝子を全くランダムに伝えることになる。

ここで問題になるのは，両親のいずれの遺伝子型が平均的に子世代に伝わるかということである。

そこで，育種価 breeding value という概念が定義される。

育種価とはその字のごとく育種計画における動物の価値を表す用語である。育種価は集団平均に対する後代の能力を表わす尺度である。

単一遺伝子座を例にとれば，各遺伝子型の育種価は後代の集団平均からの偏差を2倍して求められる。後代の偏差を2倍する理由は，後代が両親の遺伝子の半分だけをもっているためである。
すなわち，後代が示す集団平均に対する偏差自体が両親の遺伝的能力を示し，それが育種価の1/2に相当する。

いま，遺伝子型B₁B₁をもつオスを次のメスの集団に交配したとする。

 

子世代に期待される遺伝子型頻度は父親と母親の遺伝子プールからの対立遺伝子間の組み合わせの確率から計算できる。
遺伝子型B₁B₁をもつオスでは，B₁遺伝子の確率は1で，B₂遺伝子のそれは0である。
メスの遺伝子プールでは，B₁遺伝子が引き出される確率はpで，B₂遺伝子のそれはqとする。

この場合の後代におけるB₁B₁の頻度は，
P(オスからのB₁)P(メスからのB₁)＝p

B₁B₂の頻度は
P(オスからのB₁)P(メスからのB₂)＝q
と計算される。

したがって，後代の遺伝子型頻度と遺伝子型値は次のようになる。

遺伝子型B₁B₁をもつオスの後代の期待される平均値μ₁₁は，遺伝子型頻度とそれに対応する表現型値の積の総和で求められる。
μ₁₁＝f(B₁B₁)P₁₁＋f(B₁B₂)P₁₂＋f(B₂B₂)P₂₂
＝p(m＋a)＋q(m＋d)＋0(m－a)
＝m＋pa＋qd

遺伝子型B₁B₁をもつ雄の育種価BV11は，その雄の後代の平均値が示す集団平均からの偏差の2倍である。
すなわち，
BV₁₁＝2(μ₁₁－μ)
＝2[m＋pa＋qd－m－a(p－q)－2pqd]
＝2(qd＋qa－2pqd)
＝2[qa＋qd(1－2p)］
＝2q［a＋d(q－p)］

同様に，遺伝子型B₁B₂とB₂B₂を持つオスの育種価は
BV₁₂＝2(μ₁₂－μ)
＝(q－p)[a＋d(q－p)]

BV₂₂＝2(μ₂₂－μ)
＝－2p[a＋d(q－p)]

各式に見られる項[a＋d(q－p)]は各遺伝子型の育種価に現れる部分で，通常αで示される。

したがって，育種価は次のようにまとめられる。

α項は遺伝子置換の‘平均効果’average effect of a gene substitution と呼ばれる。

育種価は遺伝子頻度と遺伝子型値の関数である。集団が異なると，育種価と同様に遺伝子頻度も変動する。

ホルモンの例を用いて，2つの事例について検討してみよう。
まず，例題9－1でf(B₁)＝0.4の場合と，次に例題9－2でf(B₁)＝0.8の場合である。

例題9-1．B₁遺伝子の頻度　p＝0.4とすると，この集団は次のようになる。

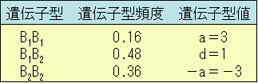
m＝9の場合の集団平均は
μ＝m＋a(p－q)＋2pqd
＝8.88

この集団における遺伝子の平均効果は
α＝a＋d(q－p)
＝3.2

したがって，育種価は次のようになる。

B₁B₁とB₁B₂をもつ親の育種価が正の値を示しているので，これらが両親となれば集団平均を増加させるだろう。

例題9-2．p＝0.8とすると，この集団は次のようになる。

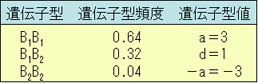
この集団は
μ＝m＋a(p－q)＋2pqd
＝11.12

α＝a＋d(q－p)
＝2.4

したがって，育種価は次のようになる。

全ての育種価がp＝0.4とした例題9-1で求められたものより小さい。集団平均を増加させると期待されるのは遺伝子型B₁B₁を持つ両親だけである。

上記2つの例題で得られた育種価を比較すると，育種価は当該の集団に特有のもので，遺伝子型頻度に依存していることが分る。

この場合の育種価間の相違は相加的 additive である。すなわち，BV₁₁とBV₁₂の差はBV₁₂とBV₂₂の差と等しく，αである。

BV₁₁－BV₁₂＝2qα－(q－p)α
＝α

また，
BV₁₂－BV₂₂＝(q－p)α－(－2pα)
＝α

このように，個体の育種価は相加的遺伝子効果といわれる。B₂B₂遺伝子型をB₁遺伝子で置き換えると，B₁B₂遺伝子型となり，育種価αの増加につながる（遺伝子置換の平均効果）。
同様に，ヘテロ接合体のB₂遺伝子をB₁遺伝子で置き換えると，その育種価はさらにα増加することになる。

9-4．優性偏差

例題9-1では，遺伝子型値と育種価はつぎのとおりであった。

育種価は両親がもつ，それぞれの遺伝子型の値である。両親がそれぞれの後代にその遺伝子の一方を伝えるので，育種価は遺伝子型を構成する各対立遺伝子の値の合計を表すと考えられる。
この時，遺伝子型値と育種価がなぜ異なるのかという疑問が生ずる。

遺伝子型B₁B₁に対する遺伝子型値V_ijと育種価BV_ijの差は次のように表せる。

V₁₁－BV₁₁＝a－2qα
＝a－2q[a＋d(q－p)]
＝[a(p－q)＋2pqd]－2q²d

B₁B₂に対しては,
V₁₂－BV₁₂＝d－(q－p)α
＝[a(p－q)＋2pqd]＋2pqd

B₂B₂に対しては,
V₂₂－BV₂₂＝－a－(2pα)
＝[a(p－q)＋2pqd]－2p²d

各式の中の[a(p－q)＋2pqd]は集団の平均遺伝子型値であり，各遺伝子型のV_ij－BV_ijの差に見られる。各式の残りの項は優性偏差 dominance deviation といい，Dijで表される。

すなわち，D₁₁＝－2q²d，D₁₂＝2pqd，D₂₂＝－2p²dとなる。

優性偏差は遺伝子型を構成する遺伝子の組み合わせによって生じる効果（相互作用による生じる値）と定義される。

したがって，遺伝子型値V_ijは次のように表記できる。
V_ij＝平均遺伝子型値＋BV_ij＋D_ij

各遺伝子型に対する種々の値を次表にまとめる。

この章の初めに個体の表現型値は以下のように表した。
P_ij＝m＋V_ij

いまこのモデルは次のように書き換えることができる。
P_ij＝m＋［a(p－q)＋2pqd］＋BV_ij＋D_ij

μ＝m＋［a(p－q)＋2pqd］なので，表現型値は次のように表すことができる。
P_ij＝μ＋BV_ij＋D_ij

例題9－3では，表現型値をそれぞれの成分に分解して考えてみよう。
ここでは，p＝0.6とすると，
μ＝m＋a(p－q)＋2pqd＝10.08
α＝a＋d(q－p) ＝2.8

したがって，

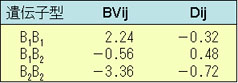
　P₁₁＝μ＋BV₁₁＋D₁₁
＝10.08 ＋ 2.24 － 0.32
＝ 12

P₁₂＝μ＋BV₁₂＋D₁₂
＝10.08 － 0.56 ＋ 0.48
＝ 10

P₂₂＝μ＋BV₂₂＋D₂₂
＝10.08 － 3.36 － 0.72
＝ 6

ホルモンの例では，これらが各遺伝子型に対する表現型である。

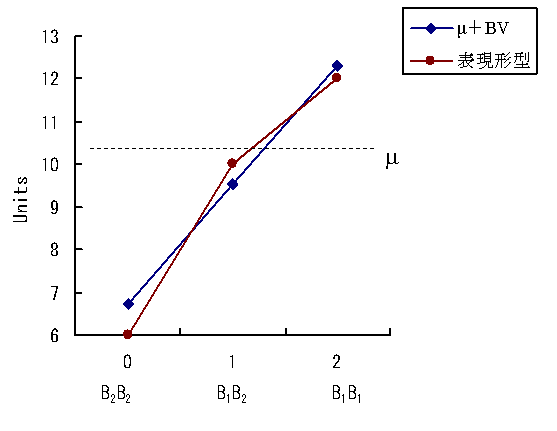
右図は，p＝0.6の時のホルモンの例で見てきた各遺伝子型の表現型値とμ＋BVをグラフ上に示したものである。

横軸の遺伝子型の部分には，遺伝子型に含まれるB₁遺伝子の数，すなわち左から0，1，2としてある。
グラフの傾きは遺伝子置換の平均的効果で，この例ではα＝2.8である。

表現型値とμ＋BVの差が優性偏差である。
もしdが0であれば，すべての優性偏差が0となり，その形質は完全に相加的な関係P_ij＝μ＋BV_ijを示す。

9-5．分散

集団の平均は表現型値の平均である。実際の観察値は平均値のまわりにばらつく。

例題8-1では，平均値は8.88であったが，実際の観察値は12，10または6であった。

この平均値のまわりのバラツキは分散として数値で表わすことができる。分散は通常σ²で表される。

単一遺伝子座位で表現型の分散を計算すると，
σ_P²＝ｆ(B₁B₁)(P₁₁－μ)²＋ｆ(B₁B₂)(Ｐ₁₂－μ)²＋ｆ(B₂B₂)(P₂₂－μ)² これは，平均からの偏差平方(P_ij－μ)²の加重平均である。

P_ij－μ＝BV_ij＋D_ij（育種価と優性偏差の合計）なので，表現型の分散は次のようになる。
σ_P²＝p²(BV₁₁＋D₁₁)²＋2pq(BV₁₂＋D₁₂)²＋q²(BV₂₂＋D₂₂)²

この式を展開してまとめると，次のようになる（計算の詳細は省略します）。
σ_P²＝2pqα²＋(2pqd)²

2pqα²は育種価の加重平方和であり，これは当該集団における動物間にみられる育種価の変動に関与するσ_P²の全体の分散の程度を示す。

育種価の変動は相加的遺伝分散 additive genetic variance と呼ばれ，σ_BV²またはσ_A²のいずれかで表わされる。

(2pqd)²は当該集団における個体間の優性偏差の加重平方和である。優性偏差のバラツキは優性分散と呼ばれ，σ_D²で表される。

したがって，
σ_P²＝σ_A²＋σ_D²
となる。

単一遺伝子座にある遺伝子によって発現する形質を考えた時，σ_A²＋σ_D²はともに遺伝分散を示し，σ_G²で表される。

この場合，非遺伝的な分散を考慮にいれていないので，
σ_P²＝σ_G²
である。

 

---

最初に戻る

---

メニューのページへ戻る

家畜繁殖学 家畜育種学 参考文献

February 03, 2020