9．量的形質の遺伝

このページの内容

量的形質とは 遺伝的パラメータ 遺伝率 反復率 統計学 分散 共分散 相関関係 回帰 遺伝分散の推定 正規分布

---

 

9-1．量的形質とは

家畜の経済能力，たとえば

• 乳牛の泌乳量
• 肉用家畜の増体量とか産肉量
• 卵用鶏の産卵数

などをそれぞれ測定してみると，これらの値はその家畜集団では連続的な変異としてとらえられる。

このような形質を量的形質 quantitative character と呼び，これまで見て毛色や角の有無などの質的な差異のような不連続的変異としてとらえられる質的形質 qualitative character とは区別される。

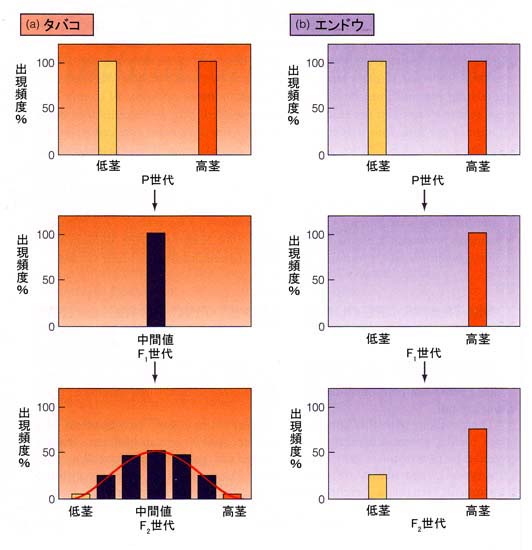
量的変異と質的変異を示す植物における例を右図に示した。

(a)はタバコの茎の高さに関する量的変異，(b)はメンデルが行ったエンドウの茎の高さの質的変異を示す。

F₁世代では，ポリジーン遺伝をするタバコの例では両親の中間値となり，エンドウの例では優性の形質のみが認められる（メンデルの優劣の法則）。

さらにF₂世代では，エンドウでは3：1に分離するが，タバコの例ではさらに変動幅が広がりいろいろな長さの茎をもつ個体が生じる。

量的形質には，次の2つの基本的な特徴がある。

1. 多数の遺伝子座上にある遺伝子によって影響されている（ポリジーン遺伝である）。
2. 部分的に環境要因の影響を受けている。

多くの場合，表現型は連続した値をとる。
量的形質の遺伝を簡単に説明するモデルとしてヒトの皮膚の色の例を考えてみよう。

黒人と白人とが結婚した場合の子孫の皮膚の色は量的形質で示される連続的変異とそれを支配する遺伝子の関係で説明することができる。

ヒトの皮膚の色を支配する遺伝子座にはAとBの2つがあり，遺伝子AとBとはともに皮膚の色を黒色にする優性遺伝子である。

黒人と白人のF₁の皮膚の色は混血児特有の中間色となるが，混血児同士の結婚から生まれる子の皮膚の色は

黒色，暗色，中間色，淡色，白色

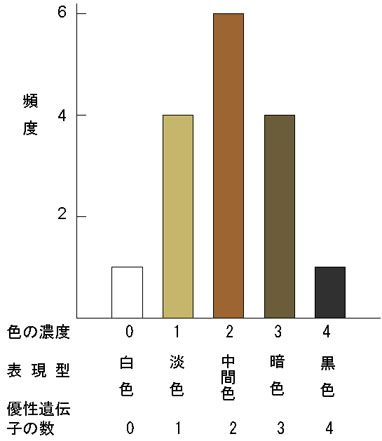
の5つに別れ，その出現頻度は1：4：6：4：1である。

この結果を，F₂の遺伝子型の分離と比べてみると，

 

AABB	黒色	1
AAbb	中間色	1
AaBb	中間色	4
aaBB	中間色	1
AABb	暗色	2
AaBB	暗色	2
Aabb	淡色	2
aaBb	淡色	2
aabb	白色	1
	合計	16

AあるいはB優性遺伝子の合計によって色の発現が異なることがわかる（右図）。

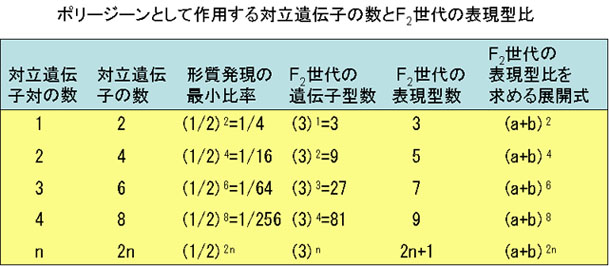
ポリージーンとして作用する対立遺伝子の数とF₂世代の表現型比との関係を次表にまとめた。

 

遺伝子対が3組ある例

ヒトの目の色

 

次のようなヒトの目の色に対するGalton（1889）の分類がある。今，これに対応した量的形質のモデルを考える。

1. 2個の対立遺伝子をもつ3つの独立した遺伝子座を想定する，すなわちG, g, H, h, I, i。
2. 各遺伝子は同じように作用し，遺伝子座間には相互作用がないものとする。
3. 各遺伝子は相加的に作用する。

 

Galtonの眼色の分類	代表的な遺伝子型	大文字で示した 対立遺伝子数
light blue blue blue-green hazel light brown brown dark brown and black	g/g h/h i/i G/g h/h i/i G/G h/h i/i G/G H/h i/i G/G H/H i/i G/G H/H I/i G/G H/H I/I	0 1 2 3 4 5 6

大文字で示した対立遺伝子をまったくもたない場合には最も明色（light blue）となり，これに対して6個もつ場合には最も暗色（dark brown and black）となる。

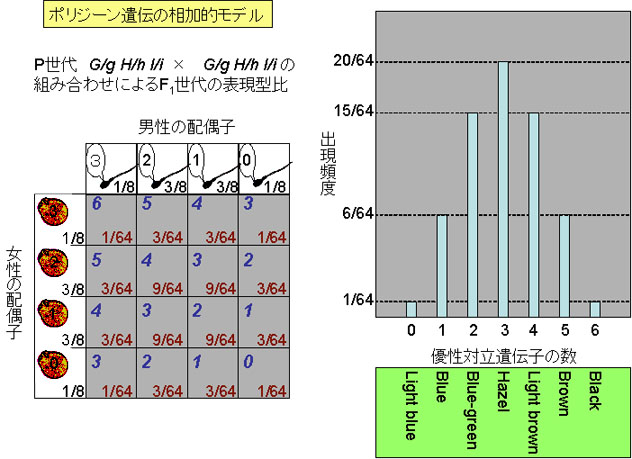
ここで，3遺伝子座ともヘテロ接合体のヒト同士の子孫に見られる目の色の分布を考えてみよう（右図）。 それぞれの配偶子には0，1，2，3個の大文字遺伝子が含まれることになるので，4×4の受精の組み合わせが考えられる。

配偶子の組み合わせによる表現型の分布比は，（a＋b）⁶を展開した係数に等しくなり，すなわち，1：6：15：20：15：6：1となる。

 

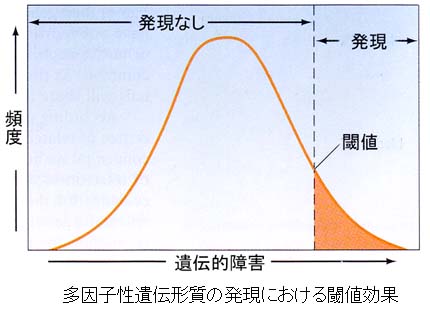
閾値形質

上記の目の色の例では表現型の分類は7種となるが，観察値や表現型が不連続な変異を示す形質でありながら，遺伝支配にいくつかの遺伝子が関与しているので量的形質として考えられているものがある。たとえば，

• ある年齢までの生存率（“生”か“死”か2つの型しかない悉無形質）
• 疾病発症（“有”か“無”の2つしかない悉無形質）

などである。
これらの形質には多数の遺伝子座上の遺伝子が関与し，環境も影響する。このような形質は閾値形質とも呼ばれる。

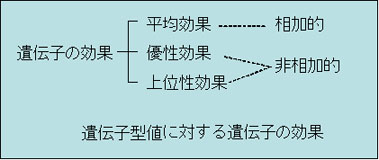
遺伝子の効果

メンデル遺伝学の基本原則は各遺伝子座間ならびに遺伝子座内における遺伝子の作用に適用される。

量的形質の遺伝子型は多数の遺伝子座上の遺伝子から構成されるが，表現型に対する個々の遺伝子座における遺伝子の作用は，遺伝子型全体の作用に比べると極めて小さい。したがって，個々の遺伝子の作用を明らかにすることも困難で，またこれらの遺伝子座の分離の法則も観察できない。

このため，量的形質を研究するためには分散という概念を理解し，遺伝的なパラメータや統計手法の知識が必要となる。

表現型は次のモデル方程式で表わすことができる。
P＝μ＋A＋D

ここで，μは平均値，Aは育種価(相加的遺伝子効果)，Dは単一遺伝子座における優性偏差である。

AとDはともに表現型に対する遺伝的貢献度を示す。 したがって，
P＝μ＋G
となる。

表現型の分散はσ_P²=σ_G²，
σ_G²を各成分に分割すると，σ_P²=σ_A²＋σ_D²となる。

任意の遺伝子型値をもつ単一遺伝子座で遺伝子頻度が判明していれば，育種価，優性偏差とそれぞれの分散が計算できる。

しかし，量的形質では表現型値に対する各遺伝子座の寄与が非常に小さく，遺伝子頻度も不明なため，それぞれの遺伝子座においてこれらの値を求めるのは困難である。

育種価は，選抜に関連する遺伝子型値の和の最も重要な成分であり，育種を進める上で，育種価の全体の表現型値に対する割合を正確に推定される必要がある。

同様に優性効果は優性偏差の和で表わされる。さらに，表現型の発現に1つ以上の遺伝子座が含まれた場合に，異なる遺伝子座上にある遺伝子同士で相互作用が生じることがある。

このような遺伝子座間の遺伝子の相互作用をエピスタシス（上位性）効果という。エピスタシス効果の和をIで示すと，
G＝A＋D＋I
となる。

遺伝的分散にもエピスタシス効果の項を追加すると，σ_P²=σ_A²＋σ_D²＋σ_I² と表すことができる。

 

環境の影響

量的形質の2つめの特性は，表現型の発現に小さく無作為な環境効果の影響がいろいろ関与することである。

環境要因は個体の遺伝子型に関係なく，新たな分散の成分として考えられる。また，体長や体重のような測定値には個体の遺伝子型に全く関係ない測定誤差も含まれる。

表現型モデル方程式にこれらの要因を加えると次のようになる。
P＝μ＋G＋E

環境（ならびに測定誤差）の影響Eは定数項μに対する正または負の偏差で表され，遺伝的でない環境要因と測定誤差の和である。

表現型は選抜を検討する際に利用できる唯一の情報であるため，上記の式は，遺伝的に優秀な個体を選抜しようとした時に有用である。

この表現型モデル方程式から，平均以上の表現型値が得られた場合にはその個体が遺伝的に優れているか，あるいは平均以上の環境効果を受けたものと考えられる。

表現型の観測値から優秀な個体を判別する正確度を増加させる情報（たとえば，後代検定など）が選抜の際に極めて有益である。

集団の表現型の分散は次のように表すことができる。
σ_P²=σ_G²＋σ_E²＋2Cov(G,E)

上式には環境分散σ_E²が含まれ，最後の項Cov(G,E)は個体の遺伝子型と環境の影響の共分散である。

共分散は2つの測定値が共にどのように変動するかを示し，負の値，0または正の値をとる。

たとえば，集団において平均以上の遺伝子型値をもつ個体が平均以上の管理（たとえば，良質の飼料や良好な健康管理）を受ければ，GとEの共分散は正となる。

しかし，この章で量的形質を考える時，個体の遺伝子型と環境要因は独立である，すなわちCov(G,E)＝0であると仮定している。

したがって，表現型分散は次式となる。

σ_P²=σ_G²＋σ_E²

 

 

9-2．遺伝的パラメータ

遺伝率 heritability

量的形質の育種価を推定する時や種々の選抜方法より期待される反応を予測する際に，遺伝率は非常に重要なパラメータである。

遺伝率には広義と狭義の定義がある。

広義の遺伝率 h_B² (heritability in the broad sense) は表現型分散に対する遺伝分散の比率と定義させる。
h_B²＝σ_G²/σ_P²

 

広義の遺伝率は，表現型分散（全体の分散）のうち集団内の遺伝子型の違い（遺伝分散）が寄与する割合を示す。

σ_P²≧σ_G²≧0なので，0≦h_B²≦1である。

狭義の遺伝率はh² (heritability in the narrow sense)で示され，表現型分散に対する相加的遺伝分散の比率として定義される。
h²＝σ_A²/σ_P²

 

狭義の遺伝率，h2は全分散のうち集団内の個体の育種価の違いが寄与する割合を示す。

σ_G²≧σ_A²なので，0≦h²≦h_B²≦1である。

遺伝率は，検討中の集団ならびに形質に特有の値を示す。
同一形質であってもそれぞれの集団における遺伝分散または環境分散のいずれかが異なると，h²も変わる。 

 

反復率 repeatability

同一個体について繰り返し測定できる形質の測定値間にみられる関連度を表す。

反復して測定できる形質とは，

• 一腹子数，
• 産乳量，
• フリース重量

などである。

反復率の考え方の基本は，測定時の遺伝子型は毎回同一であるということで，測定値は環境の影響を受けて変動することになる。

たとえば，乳用雌牛の第1泌乳期の生産性に影響する遺伝子効果はその後の泌乳期の生産性に影響する遺伝的効果と同一であると考えられる。

遺伝率と同様に，反復率は分散成分の比率として定義されるが，環境効果の2つの分散成分，すなわち

• 長期的環境効果 permanent environmental influences (PE)と
• 短期的環境効果 temporary environmental influences (TE)

の比率に依存する。PEは全ての観察値に影響する。

たとえば，乳用牛の育成期における飼料給与体系が適正でなければ乳腺の発育に影響し，それが全ての泌乳期に影響する長期的効果になる。

TEは個体の一回の観察にのみ影響する環境要因である。すなわち，それぞれの測定時に個体が有利または不利な影響を受けるかどうかはまったく偶然による。

この他に，群の飼料給与体系などの環境要因が記録に影響することがある。これらによって記録は変化するが，ここでは考慮しないことにする。

環境要因Eは次の成分に分けて考える。
E＝PE＋TE

環境分散も2成分に分けられる。
σ_E²＝σ_PE²＋σ_TE²

したがって， 　　σ_P²＝σ_G²＋σ_PE²＋σ_TE²

反復率(r)は

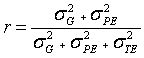
となる。

上式の分子は遺伝子型効果と長期的環境効果の分散を含んでおり，それらは一定で記録によって変化はしない。

分母は表現型に関わる全分散σ_P²である。
また，分子に相加的な分散成分σ_PE²が含まれるので，r≧h_B²である。

反復率はすでに記録をもっている個体についてその後の成績を推定するために用いられる。

 

 

9-3．統計学

量的形質に関する遺伝学の基本として，変異の大きさは分散 variances により，変異間の関連の強さおよびその方向は共分散 covariance により表される。

ここでは，表現型の分散と共分散の推定の方法，単回帰と相関係数への利用，遺伝率と反復率とこれらの統計値との関係について紹介する。

 

分散

形質の分散は次式で求められる。

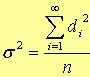
ここで，nは観察値の数，dは観察値の母平均からの偏差。

分散は偏差平方和（平均からの偏差の二乗和）の平均値である。

そして，偏差が負の値をとったとしても，その平方は正の値となる。したがって，どの分散も0または正の値をとる。

上式の母集団の分散σ²と平均値（母平均）は既知の場合を想定しているが，一般には未知であるから標本データから推定して標本分散と標本平均を定義して代用されることが多い。

すなわち，標本平均は，

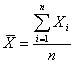
標本平均を用いて標本分散を求めると，

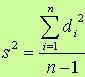
ただし，偏差dは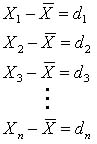 　　

である。

上式の標本平均は分散を推定するために用いられた同一標本に従属しているので，分母から1が引かれている。s²は母集団分散の推定値である。

分散の平方根は標準偏差 standard deviation と呼ばれる。

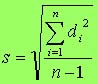
標準偏差は正規分布を描く時に平均値とともに用いられるパラメータである。

 

共分散

共分散は，2つの変数がどのように変動するかを表わす量である。

変数XとYがある時，共分散はs_XYと表記され，次の式で求められる。

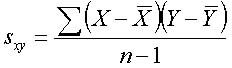
XとYは同一個体で観察される2つの形質や，表現型に対するGとEの共分散を考えた時のように同一形質に影響する2つの成分などである。

この式から，以下のことがいえる。

1. Xが平均値より大きいとYとともに平均値より大きければ， s_XYは正の値をとる。
2. Xが平均値より大きい時Yが平均値より小さければ（逆の場合も同じ）， s_XYは負の値をとる。
3. 偏差の積和が0の場合，共分散σ_XYは0。
   2つの変数が独立している場合には共分散が0となる。

 

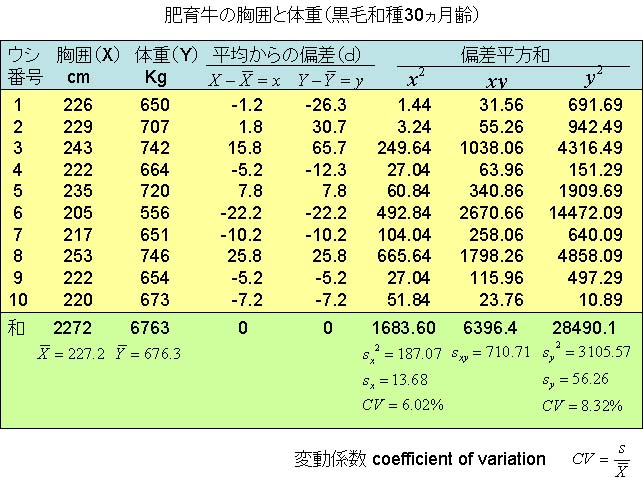
相関関係

したがって，先ほどの肥育牛の胸囲と体重のデータについて，胸囲をX，体重をYとして相関係数を計算すると，

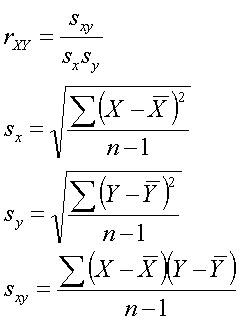
なので，相関係数r_XYは

となる。
この応用例として，育種価と表現型値の相関係数は，

遺伝率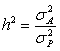なので，この相関係数は遺伝率の平方根に等しいことになる。

 

回帰

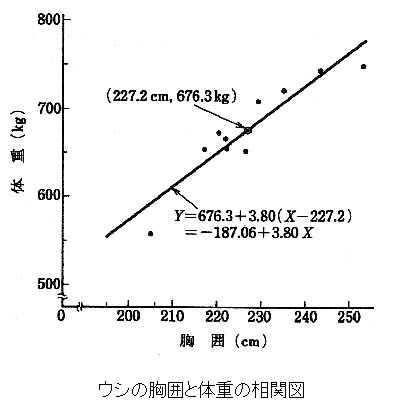
胸囲Xと体重Yとの間に相関があり，先の例のようにXが増加するにつれてYが直線的に増加するときは，

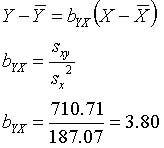
という関係がある。

これらから，回帰式を求めると，右図のようになる。

したがって，胸囲が与えられれば体重が推定できる。

このように，ある変数の値が判明している時に他の変数の値を予測したいことがある。
他の例として，第1泌乳期の乳量の記録から第2泌乳期で期待される乳量や離乳時体重から一歳時体重の予測などである。

このような予測に用いられる統計量が回帰係数 regression coefficient である。

b_Y･Xは共分散s_XYの値によって，負，0または正の値をとる。

 

回帰係数bY･Xの単位は何であろうか？

例題のように， Xが長さ(センチメートル)，Yが重さ(キログラム)で表わされる時，共分散は’長さ×重さ’で，分散は’長さの平方’で表わされる。 したがって，この回帰係数は重さ/長さの単位をもつ。すなわち，回帰係数によって形質Xが1センチメートル変化すると，形質Yが何キログラム変化するのかを予測できる。

遺伝的パラメータは回帰係数と考えることができる。たとえば，ある個体の表現型値に対する育種価の回帰係数は次式で求められる。

この回帰係数は遺伝率h²に等しい。個体の表現型から育種価を予測する方程式は，

_i＝_A＋b_A･P(P_i－_P)

ここで，_A＝0とすると，b_A･P＝h²なので，

_i＝h²(P_i－_P)

となる。

 

9-4．遺伝分散の推定

1. 回帰または相関分析から求める方法個体間の相違が相加的遺伝子によるものであるとすれば，子は親に似るはずである。
   たとえば，回帰係数b，または相関係数rは
   
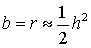
2. 分散分析から求める方法父親が同じであるための似通いによって生じた分散（σ_s²）比を求める。
   たとえば，
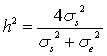   ただし，σ_e²はその他の分散。

 

9-5．正規分布

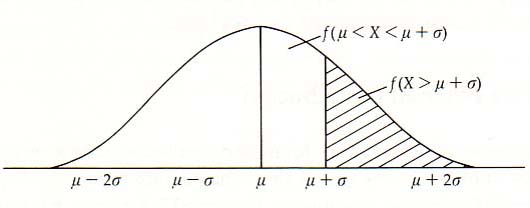ほとんどの量的形質の観察値をかなり多くグラフ上にプロットすると，観察値の頻度は右に示したような正規分布の特徴である釣り鐘型を示すようになる。

 

正規分布の特徴

• 観察頻度の和は1に等しい。
• したがって，曲線の下につくられる面積は1に等しい。

正規分布は母平均μを中心に左右対称で，母平均μと特定の領域μ＋tの間の観察頻度は母平均μと特定の領域μ－tの間の頻度と同一である。

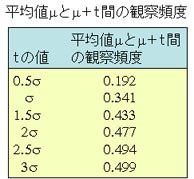
右の表はμと標準偏差が0.5ずつ増加したt間の観察頻度を示す。

表から，

• μ－σとμ＋σ間の頻度は0.682
• μ－2σとμ＋2σ間の頻度は0.954
• μ－3σとμ＋3σ間の頻度は0.998

と計算できる。

これらの頻度は，正規分布は左右対称なため右表の値の2倍となる。

 

---

最初に戻る

---

メニューのページへ戻る

家畜繁殖学 家畜育種学 参考文献

February 03, 2020