11．育種価の予測

このページの内容

選抜のねらいは改良しようとしている集団における望ましい遺伝子の遺伝子頻度を高めていくことである。したがって，採用した選抜基準もそのねらいどおりの基準でなくてはならない。

この点で，量的形質の場合は選抜の対象と各個体がどれほど多くの望ましい遺伝子を持っているかを直接見たり，数えたりすることができないので，予測育種価が選抜基準の評価に用いられる。

すなわち，表現型値を手がかりとして，育種価をいかに正確に予測するかが量的形質の選抜を進めていく上で重要となる。

11-1．育種価

前章では遺伝子効果を3つの成分に分割して考えた。

個々の遺伝子の相加的な遺伝子効果の和
各遺伝子座上にある遺伝子の相互作用，すなわち優性効果の和
異なる遺伝子座における遺伝子の組み合わせによる作用，すなわちエピスタシス効果の和

このうち，後代にそのまま遺伝されるのは相加的遺伝子効果である。

その理由は，以下の通りである。

優性効果は遺伝子座上の特有の遺伝子の組み合わせによって生じるので，親はその子供に優性効果を直接伝達することはできない。各親は各遺伝子座上の遺伝子を1種類だけ伝達するだけである。
エピスタシス効果は異なる遺伝子座における遺伝子の組み合わせによるもので，独立分離の法則によって次世代に必ず伝達されるものではない。

そこで，各遺伝子型における相加的遺伝子効果の和を育種価と呼ぶ。すなわち，育種価は親が次世代へ寄与する平均の遺伝的価値を示す。

11-2．最良線形予測法

遺伝率，反復率，遺伝相関などの遺伝的パラメータが知られていて，しかも集団平均値が既知であるか，あるいは選抜の対象となっている個体がすべて同一時期に同一の条件のもので飼育されている場合，育種価の予測に以下に述べるような最良線形予測法 best linear prediction が用いられる。

11-2-1．個体自身の1回記録にもとづく育種価の予測

発育能力，飼料利用能力などのように選抜対象の個体自身について表現型値が得られる場合を考えてみよう。

ここで，遺伝子型値が集団平均μと育種価ｇとの和であり，非相加的効果と環境効果を合わせてeとすると，表現型値は次式により表される。
Y＝μ＋g＋e

いま，表現型値を集団平均からの偏差と考えると，
Y－μ＝g＋e
となる。

得られた表現型値から未知の育種価を予測するということは，育種価ｇの表現型値Y－μに対する回帰直線式を求めることになる。

回帰係数はその定義から，

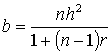
と計算される。ここで，nは記録の数である。

いま，1回の記録にもとづく例を考えているのでn＝1を代入すると，

b_g･(Y-μ)＝h²

となり，次の育種価予測式が導かれる。

g＝h² (Y－μ）

すなわち，育種価は表現型値の集団平均からの偏差に遺伝率を乗ずることによって予測される。

例題11-1　ある雄牛AとBの1歳齢体重がそれぞれ430kgと420kgであったとする。

1歳齢体重の集団平均が390kgで，遺伝率が0.63であるとすれば，これらの雄牛の育種価は次のように予測される。

＝0.63×(430－390)＝＋25.2kg
＝0.63×(420－390)＝＋18.9kg

この結果から，雄牛AのほうがBより遺伝的に優れていると判断される。

集団平均が知られていない場合には，同一時期に同一条件下で飼育されたすべての雄牛の1歳齢体重を集団平均の代わりに用いる。

11-2-2．個体自身の複数回記録にもとづく育種価の予測

泌乳量，産毛量，子牛の離乳時体重，一腹子数などのように，同一個体について繰り返し測定値が得られる場合も同様に，次の育種価予測式が得られる。
g＝b(Y－μ）

ここで，前出のとおり

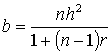
例題11-2　次の個体の育種価を比較してみよう。

遺伝率h²＝0.25
反復率r＝0.50
表現型分散σ_P²＝4,000,000
したがって，相加的遺伝子分散σ_P²＝1,000,000集団の平均(単位kg)

測定値，μ＝14,000
将来の予測値，μ’＝16,000

以下の2頭について評価しようとした場合，個体1は1回の記録をもつ。すなわち，P_1,1＝15,000
個体2は3回の記録の平均値をもつ。 _2,3＝14,800

〈自身の記録をもつ個体１の評価〉
g₁＝h² (P_1,1－μ)
＝0.25×(15,000－14,000)
＝250

〈3回の平均値をもつ個体2の評価〉
g₂＝{nh²／[1+(n-1)r]} (_2,3－μ)
＝0.375×(14,800－14,000)
＝300

1回の記録をもつ個体1は3回の記録をもつ個体2に比べ平均値は大きいが，
重み付け値に対する測定数の影響のために，個体2の記録に対する重み付けが大きい。

11-2-3．後代記録からの相加的遺伝子型値の予測

後代検定成績もとづいて候補種雄畜の育種価gは，次式により評価ができる。

Pは後代の数である。後代の数が多くなるにつれ，重み付け値は2に近似する。

例題11-3　2頭の肉用種雄牛の相加的遺伝子型値を予測する。

遺伝率h²＝0.25
表現型値の分散σ_P²＝720
したがって，σ_A²＝180

種雄牛3は50頭の後代をもち，その離乳時の平均体重は200kgである。
離乳時の集団平均は180kgである。

種雄牛4は5頭の後代をもち，その離乳時の平均体重は296kgであり，集団平均は270kgである。

半きょうだいの後代P頭からの種雄牛の相加的遺伝子型値の予測のための重み付けは次式のようになるので，

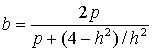
h²＝0.25を代入して，b＝2P／P＋15

この式は，それぞれの種雄牛がもつ後代の数が異なっている場合にとくに意味がある。

〈50頭の後代の平均200kgをもつ種雄牛3の評価〉

g₃＝[2P／(P＋15)](_3,50－μ)
＝(100／65)(200－180)
＝30.7

〈5頭の後代の平均296kgをもつ種雄牛4の評価〉

g₄＝[2P／(P＋15)](_4,5－μ)
＝(10／20)(296－270)
＝13.0

この例のまとめ

後代の記録が異なった管理条件で得られた場合に，集団平均による補正が重要である。種雄牛3の後代の平均は種雄牛4の後代のそれに比べかなり低いが(200 vs. 296kg)，
補正された平均値はかなり似かよっている(20 vs. 26kg)。
後代の数と遺伝率が重み付けにとって重要である。種雄牛3では100/65＝1.54，一方種雄牛4では10/20＝0.50というになっている。種雄牛3の後代の集団平均からの偏差に対する1.54の重み付けは選抜指数の重み付け
がきわめて大きいことを示している（たいていの血縁個体に対する選抜指数の重み付けは通常1以下である）。

11-2-4．複数形質の記録に基づく総合育種価の予測

改良の対象としている複数形質，ここでは例として2形質の相対経済価値をそれぞれa₁とa₂，育種価をそれぞれg₁とg₂とし，それらの積和を総合育種価Hと定義する。
H＝a₁g₁＋a₂g₂

一方，2つの選抜形質についての表現型値Y₁とY₂ に対して，それぞれ重み付け値b₁とb₂の積和した指数
I＝b₁(Y₁－)＋b₂(Y₂－)
を考え，この総合育種価と指数Iとの間の相関係数rが最大になるように重み付け値b₁とb₂を求める。

たとえば，鶏における卵重EWと産卵数EPの相対的価値，それらの表現型ならびに遺伝分散と共分散から計算すると（計算の過程は省略する），
I＝0.9992EW＋0.3010EP

が得られたとする。

この例では卵重が重いほうが有利であることがうかがえる。

これを指数選抜法 selection index procedure という。

3形質以上の例を以下に示す。

○乳牛の乳量（X₁），乳脂率（X₂），無脂固形分（X₃）に関するもの。

I＝0.02285X₁＋20.193X₂＋6.0659X₃
X₁，X₂，X₃は種雄牛の後代検定における成績である。この値のもっとも高い種雄牛を選抜する。

○豚の1日平均増体量g（X₁），背脂肪の厚さ㎝（X₂），同腹豚2頭のロース断面積の平均値㎝²（X₃），同じくハムの割合の平均値％（X₄）に関するもの。

I＝0.012X₁－5.184X₂＋0.276X₃＋0.400X₄
この式では背脂肪の厚さが（－）に重み付けられている。
○卵養鶏の卵重（X₁），体重（X₂），初産日齢（X₃），産卵率（X₄）に関するもの，

I＝1.8922X₁－0.0260X₂－0.2547X₃＋1.0091X₄
ここでは体重が小さく，初産日齢が早いものが有利である。

指数選抜法のまとめ

各形質の経済的重要度から，それぞれの重み付けの値を決め，それらに対応する形質との積を求めて合計した指数値を求め，指数値の高いものを選び出す方法である。ただし，形質数が多いと効率が悪くなり，通常4-5形質以下で用いられる。

11-3．最良線形不偏予測(BLUP)法

これまでの例では，個体は同じ環境下にある群に属していると仮定されており，表現型値の個体間差は遺伝的な差異によって起こされると考えてきた。しかしながら，実際の場では同一時期に同一条件下で検定することは難しい。このような場合，単純にすべての個体の平均値を集団平均とみなして，前述のように育種価を予測することはできない。

そこで，農家，年次，季節などの環境効果をまず推定して，その環境効果を補正して，最も正確かつ偏りがない育種価を推定する手法がブラップ法best linear unbiased prediction と呼ばれ，Hendersonによって開発された。

ブラップ法には，

後代の測定値を持つ雄親の育種価を予測する父親モデル
反復記録をもつ個体の育種価を予測する反復モデル
血統中のすべての個体育種価を予測する個体モデル

がある。

なお，ブラップ法の計算法については本稿では割愛する。

11-4．生産能と将来の記録の予測

育種価の選抜はその後代へ最も遺伝的価値の高い遺伝子を伝達する動物に対して行われる。

産乳量などのような形質については，最も良い後代を得るよりも最も価値の高い将来の記録をもつ個体を選抜したいことがある。

将来の記録を予測することは，その個体が前の記録をもつ場合を除けば育種価を推定することと同じである。

集団の平均との違いとして将来の記録を予測することはG_i＋PE_iの予測に等しい。

長期的環境効果PE_iが個体の前の記録で発現しているので，その記録はG_i＋PE_iを予測するのに用いられる。
本稿では，G_i＋PE_iを生産能 producing abilityとしてPA_iで表わす。

生産能の予測は，育種価の予測と同様である。ただし，重み付け値の分子の遺伝率h2が反復率rに置き換わっている。

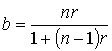
そして，生産能の予測式は
PA_i＝b(Y－μ)

n＝1の場合，重み付け値はr(反復率)となり，
PA_i＝r(Y－μ）

PA_iが集団の平均からの差を予測するので，将来の記録R_iは次式で予測できる。

R_i＝M＋PA_i

ここで，Mは予測される将来の集団平均である。

例題11-4　前出の例題11-2の記録から，これらの生産能PAと将来の記録Rを比較してみよう。

遺伝率h²＝0.25
反復率r＝0.50
表現型分散σ_P²＝4,000,000
したがって，相加的遺伝子分散σ_P²＝1,000,000集団の平均
1．測定値，μ＝14,000
2．将来の予測値，μ’＝16,000

以下の2頭について評価しようとした場合，

個体1は1回の記録をもつ。すなわち，P_1,1＝15,000
個体2は3回の記録の平均値をもつ。_2,3＝14,800

〈自身の記録をもつ個体１の評価〉

PA₁＝r(P_1,1－μ)
＝0.50×(15,000－14,000)
＝500

R₁＝M＋PA₁
＝16,000＋500
＝16,500

〈3回の平均値をもつ個体2の評価〉

PA₂＝{nr／[1+(n-1)r]}(_2,3－μ)
＝0.75×(14,800－14,000)
＝600

R₂＝M＋PA₂
＝16,000＋600
＝16,600

前出の育種価の予測と同様に，測定数と反復率により個体1の記録に対するよりも個体2の記録に対する重み付けが大きい。

最初に戻る

メニューのページへ戻る

February 03, 2020

Animal Science

A_Breeding_11.html

11．育種価の予測

11-1．育種価