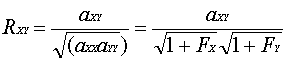13．血縁関係と近親交配

このページの内容

血縁関係を論じる場合に最も一般的に用いられる尺度が血縁関係である。

これは，2頭の動物が共有する遺伝子の割合を示す数値であり，他の動物の遺伝的価値を予測する場合に血縁の記録がどの程度信頼できるものであるかを示す尺度である。

動物の近交係数は両親の相加的血縁関係の1/2として計算される。系統交配は特定の動物と強い血縁が維持されるようにした交配システム（近親よりやや広い範囲の血縁間の交配システム）である。

このように，血縁関係を知ることによって，記録をもとに動物を選抜する際に，極端な近親交配を避けたり，望ましい動物の系統を確立するなどの場合に役立つ。

この章ではまず共通祖先の考え方について紹介し，これらの血縁関係を簡単に計算する方法を紹介する。

13-1．共通の祖先－血縁関係

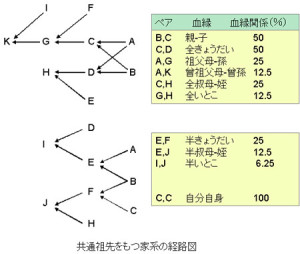
家系図と血縁関係

血縁関係（共通する遺伝子の組み合わせ）は世代毎に半減するといわれる。

動物は自分自身との血縁関係は100%となり，

親との血縁関係は50％，
祖父母とは25％，
曾祖父母とは12.5％

である。

それぞれの血縁関係を右図に示す。このように，わずか2-3世代経るだけで，先祖から子孫に受け継がれる遺伝子の割合は著しく減少することが理解できるだろう。

この半減する法則は全ての祖先がお互いに血縁関係をもたない場合に成り立つ。もし，何らかの血縁関係があれば，それを含めた複雑な計算が必要となる。

図中の用語の解説と補足は以下のとおり。

父系半きょうだい－種雄牛が同じだが，母牛が異なる場合：25％
母系半きょうだい－母牛が同じだが，種雄牛が異なる場合：25％
全きょうだい－母牛も種雄牛も同じきょうだい：50％
二卵性双子：50％
一卵性双子：100％

個体の世代ごとに，ある家系に含まれる共通の遺伝物質が半減するというのが，血縁関係を計算するための経路図をたどる方法の基礎となっている。

この方法は，対象とする個体数がさほど多くはなく，かつそれらに近親関係がない場合に計算が容易で，理解し易い。後述する近交係数は近親交配が行われる場合に遺伝子がどの程度ホモ化するかを表す尺度として考案された。

これらの方法では，当該世代よりはるか以前の任意の個体間の血縁関係は0と仮定している。この個体群は基礎集団 base population と呼ばれる。そのため，算出された血縁係数は必ずしも正確ではないが，最良の近似値と考えられる。

血縁のある個体X，Yの相加的血縁関係はa_XYで表される。相加的血縁関係は育種価を推定するために用いられる。

たとえば，XがYの親であれば，
a_XY＝0.50
となる。

動物間の血縁関係を明らかにするために家系経路をたどるという概念はライト Sewall Wright (1921)によって提唱された。

経路図をたどる方法は直系親族と傍系親族の両方に用いられる。

例題13－1a．直系親族
直系親族とは，親子間または祖父母と孫の間などの直系の血族をさす。
たとえば，個体C，G，Kが個体Aの直系子孫とすると，家系を示す矢線図は次のようになる。

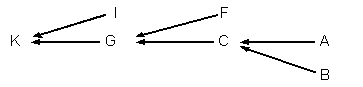
個体Aが個体Cに遺伝子の半数を伝達するので，
a_AC＝(1/2)¹＝1/2

個体Aにおける各遺伝子座の遺伝子が個体Cに伝達される確率は1/2ということになる。

個体Cが個体Gに遺伝子の半分を伝達するので，
a_AG＝(1/2)(1/2)＝(1/2)²＝1/4

個体Aにおける各遺伝子座の遺伝子が個体Gに伝達される確率は1/4ということになる。

同様に，
ａ_AK＝(1/2)(1/2)(1/2)＝(1/2)³＝1/8
例題13－1b．次のように，直系親族間に多くの経路が存在する場合がある。

直系親族間の血縁関係を計算する基本は次のようにまとめることができる。

ある動物個体からその直系祖先までの介在する世代数，すなわち経路のステップを数える。
たとえば，個体Gと個体Aとの間に3つの経路の世代数が，
n_GEA＝2
n_GEDA＝3
n_GFCA＝3
であったとする。
次のように計算する。
a_AG＝(1/2)^nGEA＋(1/2)^nGEDA＋(1/2)^nGFCA
a_AG＝(1/2)²＋(1/2)³＋(1/2)³＝ 1/2

ただし，a_EGを計算しようとした場合には，このような簡単な方法が使えない。その理由は個体Eの両親に血縁があるためである。

つまり，個体Aは個体Dの親でもあるので，Eは近親交配の子となる。祖先に近親交配が行われていた場合には，さらに複雑な計算方法が必要となる。
これについてはこの章の後半で触れるが，この血縁係数a_EGは1/2ではなく，23/32となる。

例題13－1c．傍系親族
2頭の動物が，1頭以上の共通祖先をもつが，お互いは直系の子孫ではない場合は傍系親族と呼ぶ。この場合も経路をたどる方法が利用できる。
次は血縁関係にない親AとBをもつ全きょうだいのCとDの例である。

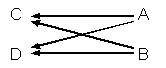
この例では，2頭の共通祖先AとBがいる。

個体Cが個体Aから特定の遺伝子を受け継ぐ確率は1/2である。
また，個体Dが個体Aから同じ遺伝子を受け継ぐ確率も1/2である。

したがって，
1/2×1/2＝(1/2)²＝1/4

個体CとDは個体Aを介した血族（全きょうだい）で，血縁関係が1/4である。

同様に個体Bを介したCとDとの血縁関係も1/2×1/2＝(1/2)²＝1/4である。
これらの2つの経路は独立しているので，2頭の共通祖先を介した個体CとDとの血縁関係は，
1/2×1/2＋1/2×1/2＝1/4＋1/4

したがって，
a_CD＝1/2
となる。

傍系親族間の血縁関係を計算する基本はそれぞれの独立した経路によって生じる血縁関係を合計することである。
先の例で示した全きょうだいの2経路の血縁係数は，

(1/2)^nCA+nAD＋(1/2)^nCB+nBD

ここで，^nCAは個体Cから共通祖先Aまでの経路の数で，^nADは個体AからDまでの経路のステップ数（矢印の数）である。
同様に，^nCBと^nBDはそれぞれ個体CからBまでと個体BからDまでの経路のステップ数である。

nの数は個体Cから共通祖先を介して個体Dに達する経路のステップの合計を示す。

したがって，
a_CD＝(1/2)^nCA+nAD＋(1/2)^nCB+nBD
＝(1/2)¹⁺¹＋(1/2)¹⁺¹
＝1/2

重要	直系親族と傍系親族に対する基本はある個体から他の個体までの経路のステップ数を計算するという点では同じだが，直系親族では共通祖先までの計算となり，傍系親族では共通祖先を介した計算となる。

動物個体の近交係数 inbreeding coefficient はある遺伝子座の2個の相同遺伝子が子孫に全く同じに伝わる確率と定義される。

これが起こり得るのは両親に血縁関係があるときだけで，この場合に両親と共通の遺伝子を子孫が受け継ぐことになる。

個体Xの近交係数はF_Xで表わし，
F_X＝(1/2)a_SxDx
となる。

ここで，a_SxDxは個体Xの父親(S_X)と母親(D_X)との相加的血縁関係を示す。

個体Ｘの自分自身に対する相加的血縁関係は
a_XX＝１＋F_X
となる。

13-2．血縁係数

血縁係数は0から1の範囲で，2個体の似通いの程度，すなわち血縁関係を示す尺度である。

血縁係数は2頭の個体における育種価間の相関係数と等しい。近親交配が行われていない個体間では，血縁係数は相加的血縁関係と同じである。

近親交配が行われている個体間では，ここで2個体をXとYとすると，血縁係数は次のようになる。

13-3．近親交配

近親交配 inbreeding が行われると，その結果生れる個体は同型(ホモ)接合体になる確率が増加する。
その程度を表すための係数を近交係数という。

最も一般に用いられている近親交配の度合いを示す方法はライトの近交係数である。

ある個体においてある遺伝子座上の2つの遺伝子(相同遺伝子)が共通の祖先遺伝から由来する確率と定義される(Malecot, 1948)。一般にFまたは f の記号で示される。
たとえば，いとこ結婚の結果生まれた子どもでは F＝1/16，またいとこ結婚では1/64である。

近交係数は次のいずれかを示すとも解釈できる。

その個体における，共通祖先と同一の相同遺伝子対をもつ遺伝子座の割合
ある特定の遺伝子座でみると，共通祖先と同じ組み合わせをもつ個体の割合

次の例のように遺伝子が同定されていたと仮定すると，近交係数は正確に計算できる。
今，どの祖先から受け継いだ遺伝子であるかが判明している5遺伝子座位を考えてみる。

遺伝子型［a₁a₈b₆b₆c₇c₈d₄d₄e₁e₆］

遺伝子a₁は祖先1から，c₈は祖先8から由来したとすると，共通祖先と同一の相同遺伝子をもつ割合は5遺伝子座のうち2つで，
F＝2/5＝0.4
である。

現実には，このように祖先からの遺伝子を同定することはできないので，他の方法によって共通祖先からの確率を計算することになる。

13-4．近親交配と遺伝子型頻度の変化

近親交配による影響を2 つの対立遺伝子をもつ1つの遺伝子座を例として考えてみる。

対立遺伝子Aとaが遺伝子頻度pとq(q＝1－p)を持つとすると，表の第2列のようなハーディ・ワインベルグの平衡に達している遺伝子型頻度を示す。

この集団に近交係数Fで近親交配が進むとすると，ヘテロ接合体の頻度が減少し，変わってホモ接合体の頻度が増加する。
2pqのヘテロ接合体が，Fの割合だけホモ接合体に変化すると考えられる。

したがって，Aaの遺伝子型頻度は次のようになる。
f(Aa)＝2pq－2pqF＝2pq(1－F)

近親交配に伴う変化

例として，初めの遺伝子頻度p＝0.6とq＝0.4，近交係数をF＝0.7とすると，近親交配前後の遺伝子型頻度は次のようになる。

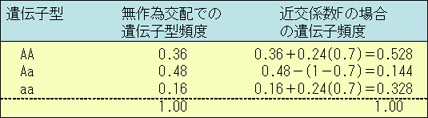
要約すると，近親交配により，

ヘテロ接合体の頻度が2pqFの割合で低下する。
各ホモ接合体の頻度がそれぞれpqFずつ増加する。
遺伝子頻度は変化しない。
近親交配が最大(F＝1)の場合は，集団は完全にホモ接合体となり，AAがp，aaがqとなる。
近交係数が最小(F＝0)で無作為交配される場合は，ハーディ・ワインベルグの法則が成立する。

13-5．近交退化

前出の表を用いて近交退化の現象を説明する。

ホモ接合体aaが個体に有害な影響を及ぼすとすれば，そのような遺伝子座をもつ個体は近親交配に伴いpqFの割合で増加する。
他の遺伝子座上にある有害なホモ接合体の頻度もそれらの遺伝子頻度に依存して増加するだろう。

これらの影響は多くの遺伝子座が平均化されて発現すると考えられるので，ほんのわずかな遺伝子座に有害な遺伝子が存在しても，近交退化が起こる。

すべての遺伝子座上で遺伝子効果が相加的であれば，極端な近交退化は起こらない。相加的な影響の場合には，ホモ接合体aaの頻度が増加して有害な影響があっても，ホモ接合体AAの頻度が増加するために生じる有益な影響によって埋め合わされることになる。

有害で劣性と考えられるホモ接合体の増加の程度は，遺伝子頻度が分れば計算できる。
たとえば，ウシにおける単蹄の劣性遺伝子の頻度をq＝1/100とすると，
ハーディ・ワインベルグの法則が成立すれば，単蹄の子牛が生まれるリスクはq²＝1/10000となる。

全きょうだい(相加的血縁関係は1/2)間で交配すると，その後代の近交係数はF＝1/4となる。前出の表に示されるように，近親交配にともない劣性ホモ接合体の頻度はq²(1－F)＋qFとなる。

この例では，およそ26/10000となる。血縁のないもの同士の交配に比べ，全きょうだい交配で生まれてくる単蹄の子牛の危険率は26倍にもなる。

近交係数はホモ接合性の尺度である。ホモ接合性が増加または減少すれば，表現型にさまざまな影響をもたらす。交配法としての近親交配の重要性については後で学ぶが，いくつかの実際の例をここに示す。

近親交配は有害な劣性遺伝子が発現する機会を増大させる。有害遺伝子の影響がでた個体やキャリアーを淘汰することによって，有害遺伝子の頻度を減少させることができる。ただし，それに関わるコストが問題となる。
近交系間の交配から得られる系統間交配 line cross は大抵ホモ型接合体の遺伝子座をもち，それによる遺伝子の優性効果が発現すれば，非近交系より優れた形質を示す。
近親交配は望ましい形質を固定するために，また均一性を達成するために利用される。たとえば，非近交系の場合に比べ近交系の子は良く親に似る。
非近交系の親と子の血縁関係は1/2であるが，近交系の親と子の場合は(1＋F)/2となる。同様に，父系または母系半きょうだいでは，非近交系の場合の1/4に対し(1＋F)/4，全きょうだいでは，同じく1/2に対し片親が近交系の場合の全きょうだいは(1/2＋F/4)，そして両親とも近交系（それぞれF_SとF_D）だが血縁関係はない場合では，同じく1/2に対し［1/2＋(F_S＋F_D)/4］となる。
血縁関係のない個体の交配により常に非近交系の子が生まれる。両親が近交系であっても血縁関係がなければ，その子は近交系ではない。

13-6．径路係数を用いた血縁関係ならびに近交関係の計算例

この章の初めに示した例を用いて，共通祖先に血縁関係がある場合を計算してみよう。

直系親族の計算例

先の例のように，個体Aと個体Gとの間の血縁関係a_AGを計算する。
それぞれの経路について個体Gと個体Aとの間の世代数(経路のステップ数)を数える。
n_GFCA＝3
n_GEA＝2
n_GEDA＝3

したがって，
a_AG＝(1/2)^nGFCA(1＋F_A)＋(1/2)^nGEA(1＋F_A)＋(1/2)^nGEDA(1＋F_A)

ここで，FAを0とすると，計算結果は先の例と同じである。
a_AG＝(1/2)³＋(1/2)²＋(1/2)³＝ 1/2

いま，ここでF_Aを0.5とすると，
a_AG＝(1/2)^nGFCA(1＋0.5)＋(1/2)^nGEA(1＋0.5)＋(1/2)^nGEDA(1＋0.5)
＝3/4
となる。

傍系親族の計算例

先と同じように，個体FとEの血縁関係を計算してみよう。

個体Fから共通祖先Aを介して個体Eまでの世代数を数える。2つの異なる経路があり，
n_FCA＋n_AE＝3
n_FCA＋n_ADE＝4

したがって，
a_AF＝(1/2)³(1＋F_A)＋(1/2)³(1＋F_A)

FA＝0であれば，
a_AF＝(1/2)³＋(1/2)³
＝3/16

FA＝0.5であれば，
a_AF＝(1/2)³(1＋0.5)＋(1/2)³(1＋0.5)
＝9/32
となる。

2個体以上の共通組成が含まれている場合には，この方法にはすべての共通祖先を介するすべての経路の和が求められる。

重要	経路が独立であるために，以下の規則に従う。ある個体は1経路につき1回だけ計算される。直系親族の場合，共通祖先に直接さかのぼって計算される。介在する個体の近交係数は無視し，各経路の共通祖先の近交係数だけを考慮に入れる。

例題13-2a．血縁関係と近交係数を求める。
例として，以下に示した全きょうだいの交配について考えてみよう。

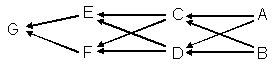
a_GEを計算するには，共通祖先C，D，A，ならびにBを介して，1つの直系親族の経路と6つの傍系親族の経路がある。

直系の経路は，n_GE＝1となり，

傍系の経路は，

傍系の経路を計算する

したがって，
a_GE＝(1/2)¹(1＋F_E)＋(1/2)³(1＋F_C)＋(1/2)³(1＋F_D)＋(1/2)⁵(1＋F_A)＋(1/2)⁵(1＋F_B)＋(1/2)⁵(1＋F_A)＋(1/2)⁵(1＋F_B)

ここで共通祖先が近交系でなければ，図からF_E＝1/4と計算されるので，
a_GE＝(1/2)(1＋1/4)＋1/8＋1/8＋1/32＋1/32＋1/32＋1/32＝1

共通祖先である個体AとBが近交系であれば，a_GEはF_AとF_Bに依存する。
a_GAを求めるためには，4つの経路があり，
n_GECA＝3
n_GEDA＝3
n_GFCA＝3
n_GFDA＝3

したがって，
a_GA＝(1/2)³(1＋F_A)＋(1/2)³(1＋F_A)＋(1/2)³(1＋F_A)＋(1/2)³(1＋F_A)
＝4(1/2)³(1＋F_A)
と計算される。

近交係数の計算例

“ある個体の近交係数はその両親の血縁係数の1/2である。”

ある個体Xの親をS_XとD_Xとすると，
F_X＝(1/2)a_SXDX
である。

したがって，経路係数法で近交係数を計算するためには，

経路をたどって両親の相加的血縁関係を計算する。
その1/2を求める。

例として，先の全きょうだいの場合で個体Eの近交係数F_Eを求めてみよう。

a_CDを計算する。
a_CD＝(1/2)^nCA+nAD(1+F_A)＋(1/2)^nCB+nBD(1+F_B)いま，F_A＝0，F_B＝0とすれば，
a_CD＝(1/2)²＋(1/2)²
＝1/2
F_Eを計算する。
F_E＝(1/2)a_CD
＝(1/2)(1/2)＝1/4

次の例題では，F_Gを計算してみる。

例題13-2b．共通先祖の1個体が近交系である場合の血縁関係と近交係数を求める。
矢線図は先ほどと同様の3世代のきょうだい交配を示す。ただし，ここではF_A＝1/4と仮定する。

個体Gの近交係数F_Gを計算する。

個体Gの両親間の血縁関係a_EFを計算する。
- EとFには4頭の共通祖先A，B，C，Dが存在する。
- 個体EとF間には，個体Aを介した2つの経路と，個体Bを介した2つの経路があり，
- さらに個体CとDを介してそれぞれ1つずつの経路がある。
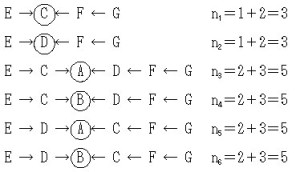
以下に6つすべての経路を示す。

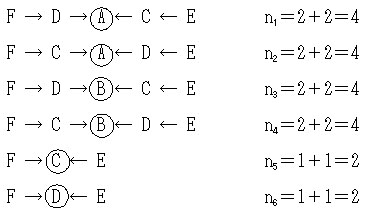
したがって，
a_EF＝(1/2)⁴(1+1/4)＋(1/2)⁴(1+1/4)＋(1/2)⁴＋(1/2)⁴＋(1/2)²＋(1/2)²
＝25/32
個体Gの近交係数は，
F_G＝(1/2)a_EF＝25/64
となる。

最初に戻る

メニューのページへ戻る

March 02, 2020