ハーディ・ワインベルグの法則
Hardy-Weinberg law
| このページの内容 |
ヘテロ接合体 ( たとえば, Bb ) である 2 つの個体を交配した場合,その結果は:
- 後代の 25% は優性遺伝子のホモ接合体である ( BB ) 。
- 50% は親と同様のヘテロ接合体である ( Bb ) 。
- 25% は劣性遺伝子のホモ接合体である ( bb ) 。そのため両親と異なり,劣性の表現型を発現する。
これが, メンデルが一因子交雑試験を行って発見した法則である
この理由は:
- 各ヘテロ接合体の親の 2 つの対立遺伝子が減数分裂によって分離する。つまり,配偶子の 50% が一方の対立遺伝子を,残りの 50% は他の対立遺伝子を運ぶ。
- 配偶子が無作為に合一すると,各 B ( または b ) をもつ卵が B ( または b ) を運ぶ精子によって受精される確率は 1/2 である(左下の表を参照)。
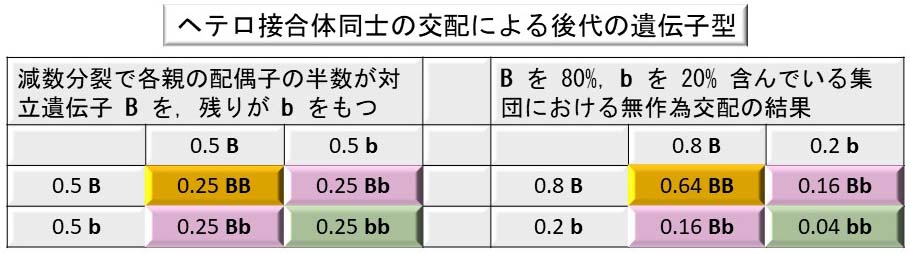
しかし,生物の集団で 2 つの対立遺伝子頻度が全く同じことはあり得ない。ここで,仮定の場合を考えてみよう。ハムスターの集団があり,そこで:
- 集団内のすべての配偶子の 80% が黒色被毛の優性遺伝子 ( B ) をもつ。
- 20% が灰色被毛の劣性遺伝子 ( b ) をもつ,とする。
配偶子の無作為な融合によって以下の次世代が生じるはずである( 上の右表 ):
- 64% ( 0.8 x 0.8 = 0.64 ) が BB ホモ接合体である。
- 32% ( 0.8 x 0.2 x 2 = 0.32 ) が Bb ヘテロ接合体である。
- 4% ( 0.2 x 0.2 = 0.04 ) が灰色被毛の ( bb ) ホモ接合体である。
したがって,この世代の 96% が黒色被毛をもち, 4% だけが灰色被毛をもつことが推定される。
灰色被毛のハムスターは最終的にいなくなってしまうのだろうか?
いいえ,いなくなることはない。その理由を詳しく見てみよう。
- BB ハムスターによって形成されたすべての配偶子は 対立遺伝子 B をもつ。
- ヘテロ接合体 ( Bb ) のハムスターによって形成される配偶子の半数は対立遺伝子 B をもつ。
- したがって,この世代によって形成される配偶子の 80% ( 0.64 + 0.5 × 0.32 ) はB をもつ。
- 灰色被毛 ( bb ) のハムスター ( 4% ) のすべての配偶子は b を含む。さらに
- ヘテロ接合体 ( Bb ) のハムスターの配偶子の半数も同様である。
- したがって,配偶子の 20% ( 0.04 + 0.5×0.32 ) が b をもつことになる。
初めの状況と同じ解答が得られたことになる。集団内の対立遺伝子 b の割合は同じままである。ヘテロ接合体のハムスターがいる限り,各世代に灰色被毛のハムスターが出現することになる。
さて,ここで二項式展開 ( p+q )2 を用いて,同じ問題を考えて見よう。
(p+q)2 = p2 + 2pq + q2
- 集団内の遺伝子総数はその集団の 遺伝子プール(遺伝子の集合として交配可能な集団)といえる。
- 今,遺伝子プールの 1 つの遺伝子の頻度を p ,その対立遺伝子の頻度を q とすると,
- p + q = 1
- p2 = 1 つ目の遺伝子をホモでもつ個体の集団内での割合
- q2 = 2 つ目の遺伝子をホモでもつ個体の集団内での割合
- 2pq = ヘテロ接合体の割合
- 我々の例題では, p = 0.8, q = 0.2 なので,
( 0.8 + 0.2 )2 = ( 0.8 )2 + 2 ( 0.8 ) ( 0.2 ) + ( 0.2 )2 = 064 + 0.32 + 0.04
この代数式によって,データを詳しく分析できる。我々の例では,B を完全優性としたので,遺伝子プール内における B と b の頻度を知る唯一の方法は,劣性形質( 灰色被毛 )の頻度を決定して,それから q の値を計算することである。
q2 = 0.04, したがって遺伝子プール内の b の遺伝子頻度は q = 0.2 である。 p + q = 1 なので, p = 0.8 ,すなわち B の遺伝子頻度は遺伝子プール内の 80% に達する。 B は b に対して完全優性なので,われわれは表現型から Bb ハムスターと BB ハムスターを識別できない。しかし,展開式の第二項 ( 2pq ) を用いると,ヘテロ接合体のハムスターの割合を求めることができる。 2pq = ( 2 ) ( 0.8 ) ( 0.2 ) = 0.32
したがって,どんなに個体数が少なかったとしても,劣性遺伝子が集団から失われることはない。
ただし,ある特定の条件を満たしていればである( これについては後述する )。
交配が無作為に行われている集団では,遺伝子頻度 gene frequencies ならびに 遺伝子型頻度 genotype ratios は代々一定である。
これは,ハーディ・ワインベルクの法則 Hardy-Weinberg law として知られている。集団遺伝学,ひいては進化に対する二項式展開の重要性を初めて示した二人に敬意を表して名前を付けている。
進化には遺伝子プールの変化が必要である。 Hardy-Weinberg の平衡に達している集団では変化は見られない。この法則によって,集団が多様性の源を維持していることの重要性を教えてくれる。 つまり, 将来必要になった時には,遺伝子プールが変化できるということである。もし,劣性遺伝子が消失する傾向があれば,集団はすぐにホモ接合体になってしまう。Hardy-Weinberg の条件下では,選択の価値がない遺伝子でも保持される。
Hardy-Weinberg の法則が適用されない場合
進化に深くかかわる変異の出現機構について考えるために,Hardy-Weinberg の法則が適用されない場合を検討しなければならない。これには 5 つの要因がある:
突然変異
突然変異によって B → b ( またはその逆 ) に変化すれば, 遺伝子 B とその対立遺伝子 b の頻度は Hardy-Weinberg の平衡のままではなくなる。
突然変異率は極めて低いので,突然変異だけで進化の過程を説明することはできない。
しかし,突然変異の一形態である遺伝子(またはゲノム全体)の 重複 duplication は,進化において重要な役割を果たしてきたと思われる。
とにかく突然変異は生物の遺伝的変異を維持・増加する機構の 1 つである。突然変異遺伝子とそれまでの遺伝子プールに含まれるものといろいろな組み合わせが試された後に,自然淘汰が働くということはあり得るだろう。
遺伝子流動
多くの種は,地域の集団から成立し,その個体は群内で交配する。各地域集団が他の集団と明らかに異なる遺伝子プールを発達させる。
しかし,ある集団に属す個体が,同一種の他の集団からの移入個体と交配することがある。これによって,その集団内に新しい遺伝子が導入される,あるいは既存の遺伝子頻度が変更されることになる。
多くの動植物で,遺伝子移入は同一種内の小集団間にばかりでなく,異種間 ( ただし,多少とも近縁の種間 ) にも起こる。 これは,雑種形成 hybridization と呼ばれる。この雑種が親世代になれば,新しい遺伝子が前の世代の遺伝子プールに加わることになる。これを 遺伝子移入 introgression という。これは,種内でというよりは種間の遺伝子流動である。
いずれの場合にも,遺伝子移入によって遺伝子プールの多様性が増大する。
遺伝的浮動
既に見てきたように,異種交配は地域集団の構成個体に限定される。もし集団が小さければ, Hardy-Weinberg の法則が適用されない 。
集団の大きさに不釣り合いに,機会的に特定の個体が排除されてしまうことがあるかもしれない。そのような場合,対立遺伝子の頻度は高い方向へ,あるいは低い方向へ機会的に浮動することがある。最終的にその対立遺伝子が集団の100%を占めるか,あるいは 消失してしまうことも起こり得る。
機会的浮動は進化的な変化となり得るが,新しい集団が元の集団よりも環境に適合しているとは限らない。機会的浮動による進化は当てがなく,適応性があるとはいえない。
| 多型との関連について
|
作為交配
Hardy-Weinberg 平衡が成立するためには,集団内の交配が無作為でなければならない。もし個体 ( たいてい雌 ) が選抜されれば,良いと思うものだけが選ばれる。ダーウィン Darwin はこれを 性選択 sexual selection と呼んでいる。
作為交配は極めて一般的に見られる。縄張り,求愛行動,社会的序列などによる。このような場合に,それぞれの個体が次世代に対して均等に貢献することはあり得ない。
類別交配 Assortative mating
ヒトにおいて無作為交配はあり得ない。自身に似た表現型( 背の高さ,年齢,民族性など )を好み結婚する。これは類別交配 assortative mating と呼ばれる。(Drawing by Koren © 1977 The New Yorker Magazine, Inc.)

近親者間の結婚は類別交配の特別な例となる。親類関係が近ければ近いほど,より多くの対立遺伝子を共有することになり,近親交配 の程度が大きくなる。近親交配は遺伝子プールを変化させる。これは,近親交配のために 同型接合性 homozygosity に成りやすいためである。両親には現れなかった,潜在的な有害劣性遺伝子が子世代で自然淘汰の試練に曝されることになる。
動物でも植物でも,多くの種で近親交配を避ける機構をもっている。例:
- 植物における 自家不和合性
- 雄マウスは相手を選ぶ時,嗅覚によって近親個体を判別する。幼時に学習 ( インプリンティング = 刷り込み ) する。 判別される臭いは:
自然選択
ある遺伝子をもつ個体が,それらをもたない個体より成熟後代を多数生産したとすると,これらの遺伝子の頻度は増大するだろう。遺伝子プールを変化させるという点では,これはダーウィンの自然淘汰説の簡単な説明になる。自然淘汰は,
- 死亡率の差異,ならびに/または
- 生殖能力の差異
死亡率の差異
特定の遺伝子型をもつ と,生殖期間が満了するまで生存している個体に比べ,生存期間が短い場合がある。
新たな受精からその生物の生殖期間が終了するまで,死亡率が違うと選択圧となるだろう。死亡率の差異は,生存への適応性に対するダーウィンの一つの判定基準(生存率)でもある。
ヒトにおける死亡率の差異に関する例:プリオンタンパク質の例はこちら, Hardy-Weinberg の平衡から大きく逸脱する例である。
生殖能力の差異
ある表現型 (すなわち,ある遺伝子型) が多くの子孫を生み出すことによって,次世代の遺伝子プールに対して過度に影響することがある。このような生殖能力の差異もダーウィンがいう適応性を示す別の判定基準(家系の大きさ)となる。
ダーウィンによると,少しでも有利な変異をもつ個体(適者) が生き残り,さらに繁殖する。それらの子孫が増えれば,親の代より影響が大きくなる。その結果,その集団における遺伝子頻度が徐々に変化することになる。.
遺伝子頻度に対する自然淘汰の影響を計算する
遺伝子頻度に対する自然淘汰の影響が計算できる。次の集団を仮定して計算してみよう:
- 36% 優性ホモ接合体 (AA)
- 48% ヘテロ接合体 (Aa)
- 16% 劣性ホモ接合体 (aa)
この集団の遺伝子頻度は,
p = 0.6 と q = 0.4 となり,
ヘテロ接合体は優性ホモ接合体と同じように生殖できるものとし,劣性ホモ接合体はその 80% とする。すなわち, AA ( または aa ) をもつ個体は 100 個体生殖できるのに対して, aa をもつ個体は 80 個体しか生殖が成功しないこととする。劣性表現型質の適応度 ( w ) が 80% または 0.8 ということにする。
この相対的な不利益は 淘汰値 selection coefficient ( s ) と呼ばれる。ここでは,
s = 1 – w
この例では, s = 1 – 0.8 = 0.2 となる。
1 世代後の優性対立遺伝子の頻度 (Δp ) における 変化 は,次の項式で表わされる。
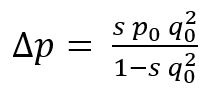
すなわち, p0 と q0 はそれぞれ優性ならびに劣性対立遺伝子の初めの頻度を示す。 各値を代入すると,
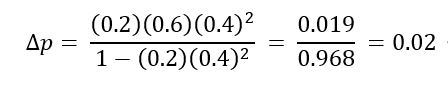
したがって,1 世代に, A の遺伝子頻度はその初めの頻度 0.6 から 0.62 へ増加し, a の遺伝子頻度は 0.4 から 0.38 へ減少する ( q = 1 – p ) 。
新しい平衡が成立すると,
- 38.4% 優性ホモ接合体 ( 2.7% の増加 ) ( p2 = 0.384 )
- 47.1% ヘテロ接合体 ( 0.9% の減少 ) ( 2pq = 0.471 )
- 14.4% 劣性ホモ接合体 ( 1.6% の減少 ) ( q2 = 0.144 )
劣性ホモの接合体の適応性が変化しなければ,世代の数だけ計算を繰り返すことができる。そのようにすると,劣性遺伝子型頻度が減少するが,遺伝子 a を遺伝子プールから除去する 割合 が低下するのが分かるだろう。すなわち,対立遺伝子 a を消滅させる効率が悪くなっていくのである。これは,ヘテロ接合体が存在する場合,遺伝子 a が淘汰の影響から保護されるためである。
March 20, 2020